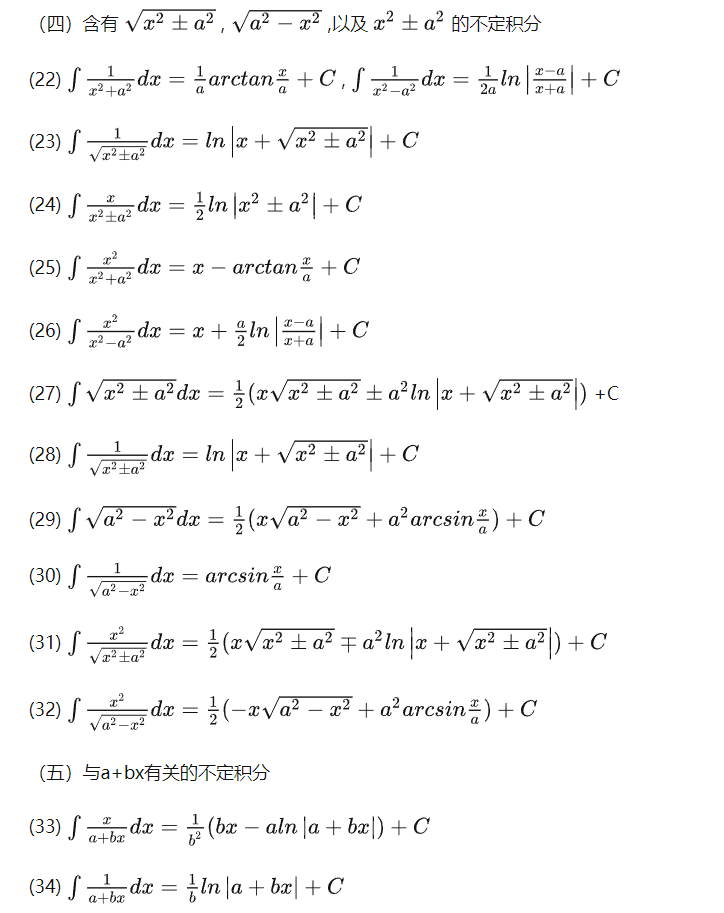AdvancedMathematics
前言
仅仅记录高等数学遇到的常见的一些我记不住的玩意
高等数学长这样

常见的积分表
$$
看得见我吗
$$
$$
(1)\int x^{n}dx=\frac{x^{n+1}}{n+1}+C ( n\ne-1 )
\
(2) \int\frac{1}{x}dx=ln\left| x \right|+C
\
(3) \int a^{x}dx=\frac{a^{x}}{lna}+C
特别地 \int e^{x}dx=e^{x}+C
\
(4) \int lnxdx=xlnx-x+C
\
(5) \int sinxdx=-cosx+C ; \int cosdx=sinx+C
\
(6) \int sec^{2}xdx=tanx+C ; \int csc^{2}xdx=-cotx+C
\
(7) \int secxtanxdx=secx+C ; \int cscxcotxdx=-cscx+C
\
(8) \int tanxdx=-ln\left| cosx \right|+C ; \int cotxdx=ln\left| sinx \right|+C
\
(9) \int secxdx=ln\left| secx+tanx \right|+C ; \int cscxdx=ln\left| cscx-cotx \right|+C
\
(10) \int \frac{1}{\sqrt{1-x^{2}}}dx=arcsinx+C
\
(11) \int \frac{1}{1+x^{2}}dx=arctanx+C
\
(12) \int arcsinxdx=xarcsinx+\sqrt{1-x^{2}}+C ; \int arccosxdx=xarccosx-\sqrt{1-x^{2}}+C
\
(13) \int arctanxdx=xarctanx-\frac{1}{2}ln(1+x^{2})+C
\
(二)与三角函数有关的不定积分
\
(14) \int sin^{2}xdx=\frac{1}{2}(x-sinxcosx)+C ; \int cos^{2}xdx=\frac{1}{2}(x+sinxcosx)+C
\
(15) \int xsinxdx=sinx-xcosx+C ; \int xcosxdx=cosx+xsinx+C
\
(16) \int \frac{1}{1\pm sinx}dx=tanx\mp secx+C
\
(17) \int \frac{1}{1\pm cosx}dx=-cotx\pm cscx+C
\
(18) \int tan^{2}xdx=-x+tanx+C ; \int cot^{2}xdx=-x-cotx+C
\
(三)与指数函数,对数函数有关的不定积分
\
(19) \int xe^{x}dx=(x-1)e^{x}+C
\
(20) \int \frac{1}{1+e^{x}}dx=x-ln(1+e^{x})+C
\
(21) \int xlnxdx=\frac{x^{2}}{4}(2lnx-1)+C
\
(四)含有 \sqrt{x^2 \pm a^2} , \sqrt{a^2 - x^2} ,以及 x^2 \pm a^2 的不定积分
\
(22) \int \frac{1}{x^2 + a^2}dx=\frac{1}{a}arctan\frac{x}{a}+C , \int \frac{1}{x^2 - a^2}dx=\frac{1}{2a}ln\left| \frac{x-a}{x+a} \right|+C
\
(23) \int \frac{1}{\sqrt{x^2\pm a^2}}dx=ln\left| x+\sqrt{x^2 \pm a^2} \right|+C
\
(24) \int \frac{x}{x^{2}\pm a^{2}}dx = \frac{1}{2}ln\left| x^2\pm a^2 \right|+C
\
(25) \int \frac{x^2}{x^2+a^2}dx = x-arctan\frac{x}{a}+C
\
(26) \int \frac{x^2}{x^2-a^2}dx= x+\frac{a}{2}ln\left| \frac{x-a}{x+a} \right|+C
\
(27) \int \sqrt{x^2\pm a^2}dx=\frac{1}{2}(x\sqrt{x^2\pm a^2}\pm a^2ln\left| x +\sqrt{x^2 \pm a^2} \right|) +C
\
(28) \int \frac{1}{\sqrt{x^2\pm a^2}}dx= ln\left| x+\sqrt{x^2 \pm a^2}\right|+C
\
(29) \int \sqrt{a^2-x^2}dx=\frac{1}{2}(x\sqrt{a^2-x^2}+a^2arcsin\frac{x}{a})+C
\
(30) \int \frac{1}{\sqrt{a^2-x^2}}dx=arcsin\frac{x}{a}+C
\
(31) \int \frac{x^2}{\sqrt{x^2 \pm a^2}}dx=\frac{1}{2}(x\sqrt{x^2 \pm a^2} \mp a^2ln\left| x+\sqrt{x^2 \pm a^2} \right|)+C
\
(32) \int \frac{x^2}{\sqrt{a^2-x^2}}dx=\frac{1}{2}(-x\sqrt{a^2-x^2}+a^2arcsin\frac{x}{a})+C
\
(五)与a+bx有关的不定积分
\
(33) \int \frac{x}{a+bx}dx=\frac{1}{b^2}(bx-aln\left| a+bx \right|)+C
\
(34) \int \frac{1}{a+bx}dx=\frac{1}{b}ln\left| a+bx \right|+C
\
$$
nnd,上面的公式不知道为啥显示不出来,那我就直接图片展示了

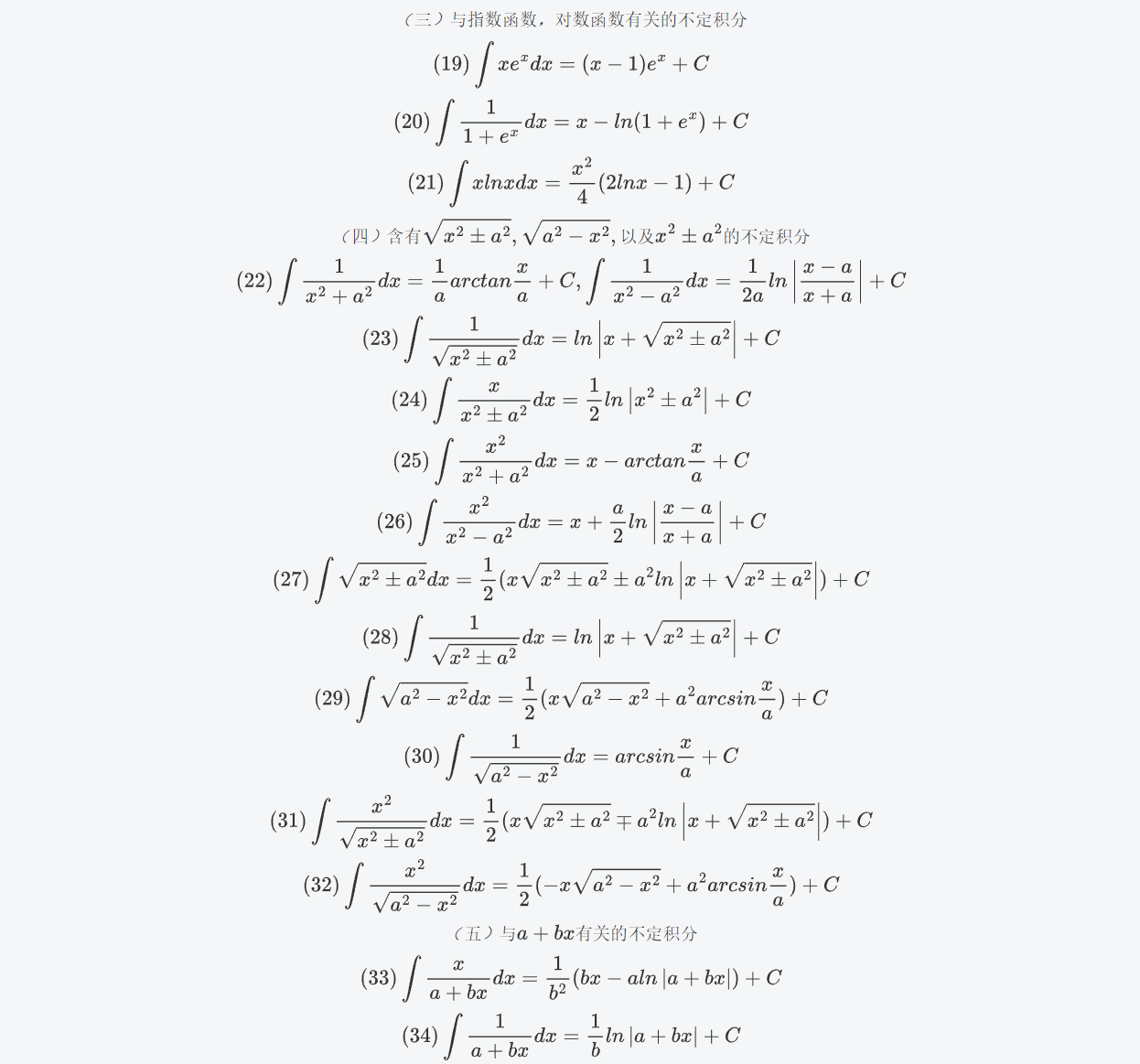
常见泰勒公式
$$
e^{x} =1+x+\frac{x^2}{2!} +\cdots +\frac{x^n}{n!} +\cdots =\sum_{n=0}^{\infty } \frac{x^{n} }{n!}
\
\sin {x} =x-\frac{1}{3!}x^{3} +\cdots +\left ( -1 \right )^n\frac{1}{\left(2n+1\right)!}x^{2n+1}+\cdots =\sum_{n=0}^{\infty}\left ( -1 \right ) ^n \frac{x^{2n+1}}{(2n+1)!}
\
\cos {x} =1-\frac{1}{2!}x^{2} +\cdots +\left ( -1 \right )^n\frac{1}{\left(2n\right)!}x^{2n}+\cdots =\sum_{n=0}^{\infty}\left ( -1 \right ) ^n \frac{x^{2n}}{(2n)!}
\
\ln{(1+x)} =x-\frac{1}{2}x^{2} +\cdots +\left ( -1 \right )^{n-1}\frac{x^{n}}{n}+\cdots =\sum_{n=1}^{\infty}\left ( -1 \right ) ^{n-1} \frac{x^{n}}{n},,-1<x\le 1
\
\frac{1}{1-x} =1+x+x^{2} +\cdots +x^n+\cdots =\sum_{n=0}^{\infty}x^n, ,\left | x \right | <1
\
\frac{1}{1+x} =1-x+x^{2} -\cdots +\left ( -1 \right )^n x^n+\cdots =\sum_{n=0}^{\infty}\left ( -1 \right )^nx^n, ,\left | x \right | <1
\
\left ( 1+x \right ) ^{\alpha } =1+\alpha x+\frac{\alpha \left ( \alpha -1 \right ) }{2} x^{2} +o\left ( x^{2} \right ),(x\to 0,\alpha \ne 0)
\
\tan x=x+\frac{1}{3} x^3+o(x^3),(x\to 0)
\
\arcsin x=x+\frac{1}{6} x^3+o(x^3),(x\to 0)
\
\arctan x=x-\frac{1}{3} x^3+o(x^3),(x\to 0)
\
由泰勒公式可以延伸出等价无穷小替换:
当x趋于0时,
\
\sin x \sim x ,; \tan x \sim x ,;\arcsin x \sim x,;\arctan x\sim x,
\
对以上公式进行处理,以下无穷小代换式:
\
x-\sin x \sim \frac{1}{6} x^3,;\tan x-x\sim \frac{1}{3}x^3,
\
\arcsin x-x\sim \frac{1}{6}x^3 ,;x-\arctan x\sim \frac{1}{3}x^3 ,
\
e^{x} -1\sim x,;\ln (1+x)\sim x,
\
a^{x} -1=e^{x\ln a} -1\sim x\ln a;(a>0且a\ne 1),
\
1-\cos x \sim \frac{1}{2} x^2,
\
(1+x)^\alpha -1\sim \alpha x ;(\alpha \ne 0).
$$
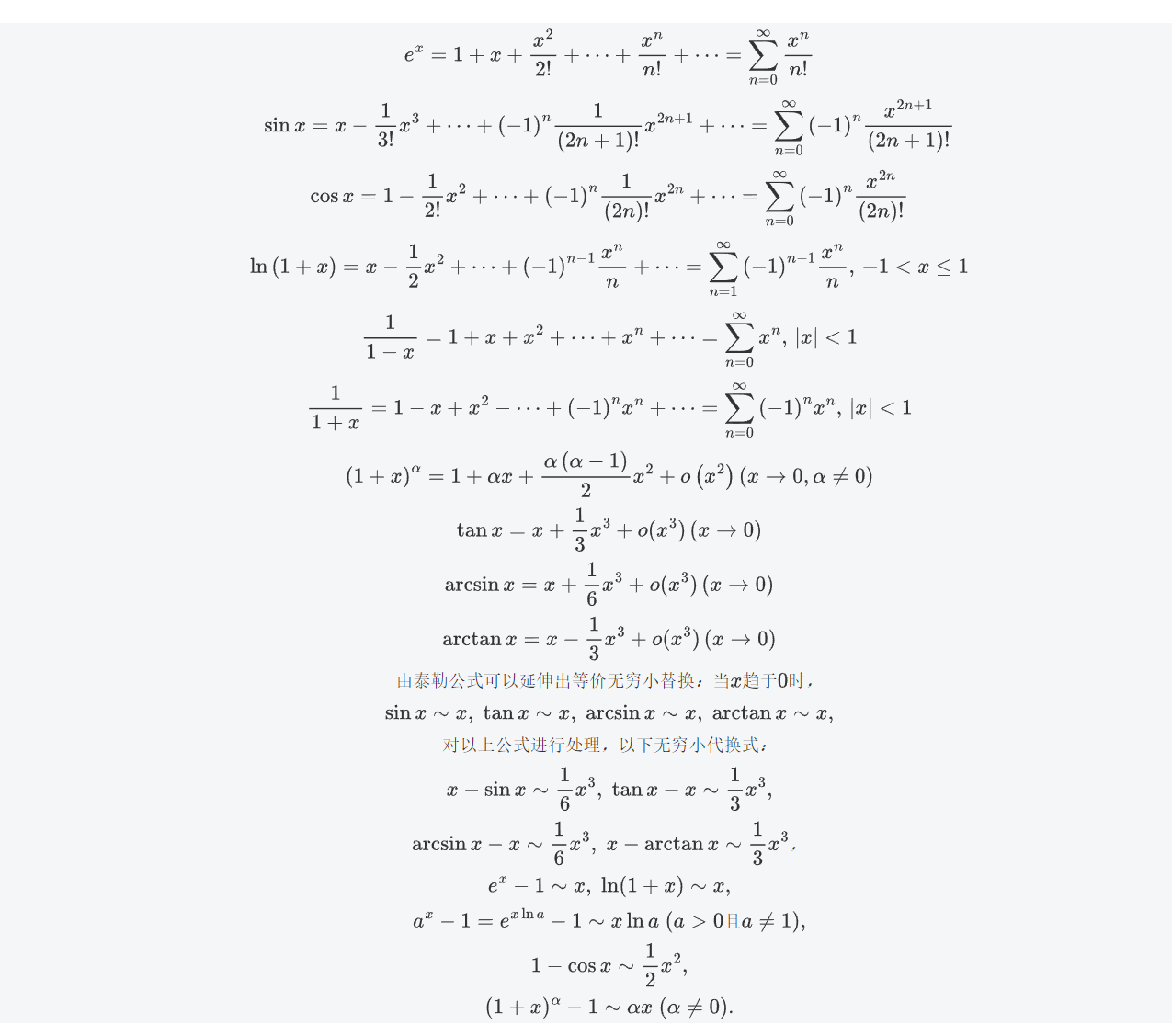
常用泰勒公式
$$
但是一般写作业用到的是以下的
\
sinx = x -\frac{x^3}{6} +o(x^3)
\
arcsinx=x+\frac{x^3}{6}+o(x^3)
\
cosx=1-\frac{x^2}{2}+\frac{x^4}{24}+o(x^4)
\
arccosx=?
\
tanx = x +\frac{x^3}{3}+o(x^3)
\
arctanx=x-\frac{x^3}{3}+o(x^3)
\
e^x = 1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+o(x^3)
\
ln(1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}+o(x^3)
\
(1+x)^{\alpha}=1+\alpha x+\frac{\alpha(\alpha-1)}{2}x^2+o(x^2)
\
\begin{align} tanx - sinx &= \frac{1}{2}x^3+o(x^3)
\
x - sinx &= \frac{1}{6}x^3+o(x^3)
\
arcsinx - x &= \frac{1}{6}x^3+o(x^3)
\
tanx - x &= \frac{1}{3}x^3+o(x^3)
\
x-arctanx &=\frac{1}{3}x^3+o(x^3) \end{align}
\
x-\ln( 1+x ) \sim \frac{x^2}{2}
\
e^x-1-x\ \sim \frac{x^2}{2}
\
1-\cos ^ax\ \sim \frac{ax^2}{2}
\
$$

泰勒补充
$$
\LARGE \begin{align} \arcsin x &= \sum_{n = 0}^{\infty} \frac{(2 n!)x^{2n+1}}{4^{n}(n !)^{2}(2 n+1)} = x+\frac{1}{6} x^{3}+\frac{3}{40} x^{5}+\frac{5}{112} x^{7}+\frac{35}{1152} x^{2}+\cdots+\frac{(2 n) !}{4^{n}(n !)^{2}(2 n+1)} x^{2 n+1}+\cdots, x \in(-1,1) \ \tan x &= \sum_{n = 1}^{\infty} \frac{B_{2n}4^{n}(4^{n}-1)}{(2 n) !} x^{2 n-1} = x+\frac{1}{3} x^{3}+\frac{2}{15} x^{5}+\frac{17}{315} x^{7}+\frac{62}{2835} x^{9}+\frac{1382}{155925} x^{11}+\frac{21844}{6081075} x^{13}+\frac{929569}{638512875} x^{15}+\cdots ,x \in(-1,1) \ \sec x &= \sum_{\pi = 0}^{\infty} \frac{(-1)^{n}E_{2n} x^{2 n}}{(2 n) !} = 1+\frac{1}{2} x^{2}+\frac{5}{24} x^{4}+\frac{61}{720} x^{6}+\cdots, x \in\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\ \csc x &= \sum_{n = 0}^{\infty} \frac{(-1)^{n+1} 2\left(2^{2 \mathrm{n}-1}-1\right) B_{2n}}{(2 n) !} x^{2 x-1} = \frac{1}{x}+\frac{1}{6} x+\frac{7}{360} x^{3}+\frac{31}{15120} x^{5}+\frac{127}{604800} x^{7}+\frac{73}{3421440} x^{2}+\frac{1414477}{65383718400} x^{11}+\cdots, x \in(0, \pi)\ \cot x &= \sum_{n = 0}^{\infty} \frac{(-1)^{n} 2^{2n} B_{2n}}{(2 n) !} x^{2 n-1} = \frac{1}{x}-\frac{1}{3} x-\frac{1}{45} x^{3}-\frac{2}{945} x^{5}-\cdots, x \in(0, \pi) \end{align}
$$
下面是网上找的比较全的: